Quorum Certified (QC) Broadcast: The Core Sub-Protocol of HotStuff
HotStuff, introduced by Yin, Malkhi et al. in [@Yin2019HotStuffBC], provides the first practical solution to the [SMR problem] with optimal communication complexity $O(n + t \cdot n)$, against $t$ actual cascading faults.
This post describes the key building block employed in HotStuff, a Quorum Certified (QC) Broadcast, depicted in Figure 1 below. The figure illustrates that a varying number of QC-phases may be chained. Indeed, the original HotStuff: Three-Chain Rules requires chaining three QC phases as a core sub-protocol operated by each leader. Later in this blog we will demonstrate the use of 2-phase QC broadcast in solving consensus.
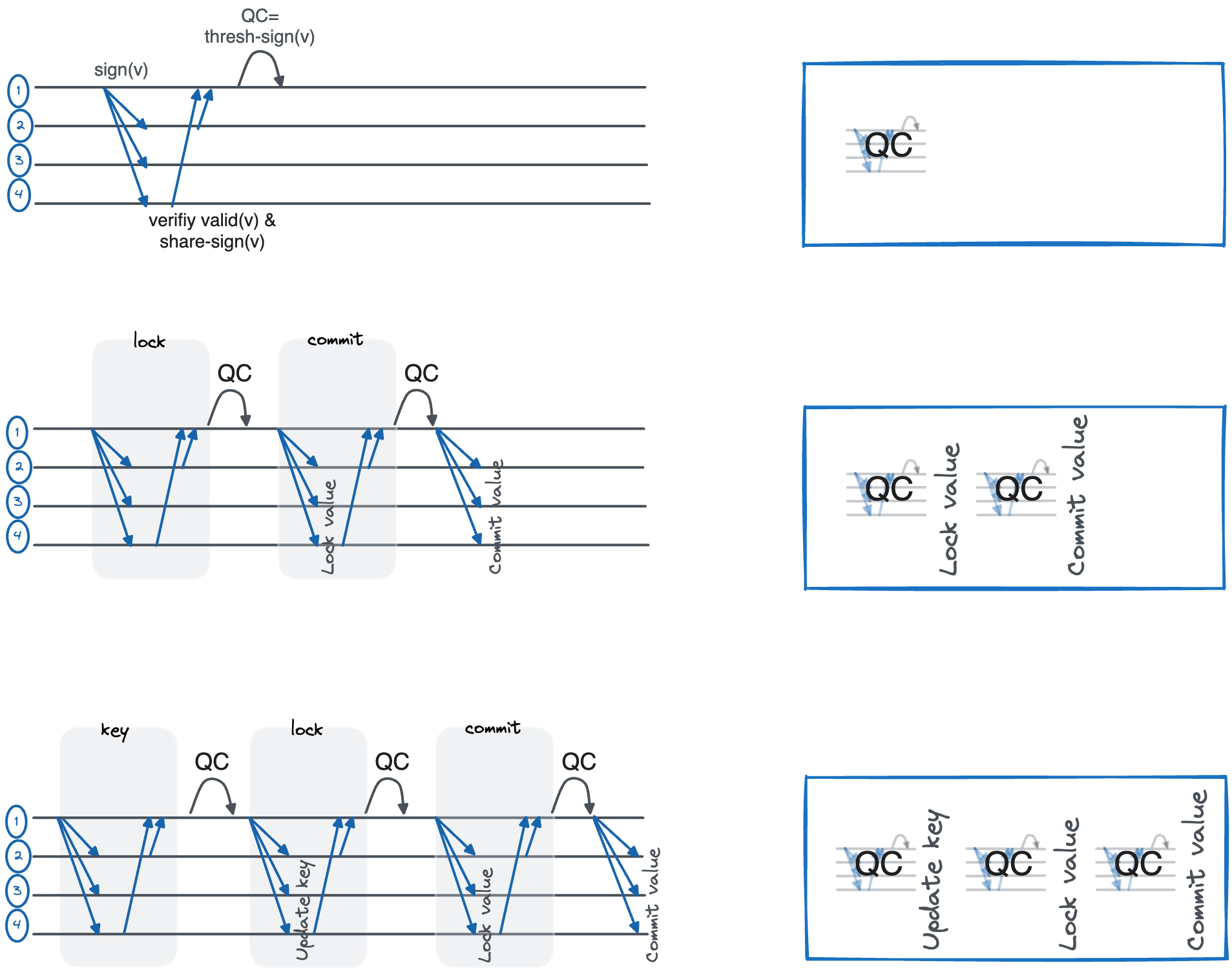
Figure 1: 1, 2 and 3 QC-phase Broadcasts (left), and QC iconic representations (right).
A single phase of the Quorum Certified (QC) Broadcast is a twist on a common building block, Consistent Broadcast (“CBC”)1. Like the CBC primitive, QC guarantees:
- (i) Agreement.
- All honest parties QC-deliver the same message by a sender, if any.
- (ii) Non-triviality.
- If a sender is honest, then eventually all honest parties QC-deliver a message from it.
Cachin et al. added in [@Cachin2001SecureAE] on top of CBC two additional properties (jointly referred to as Verifiability):
- (iii) External Validity.
- A broadcast message is accepted by parties if it satisfies a customizable application–specific validity condition, which they can verify at runtime.
- (iv) Provability.
- If an honest party QC-delivers a broadcast message, it can prove to other parties that it correctly delivered it.
1-Phase QC
A single phase of QC revolves around a CBC protocol introduced by Reiter in [@Reiter1994SecureAP]. Borrowing Reiter’s method, we can solve 1-phase QC as depicted in Figure 1 above at the top-left, and represented by a QC icon at the top-right. The protocol has linear Communication complexity, $O(n)$. A pseudo-code of QC with an optional number of phases is listed below in Algorithm 1.
Specifically, in one QC-phase , a sender invokes QC-send($m$, $V$) by broadcasting $m$ and the validity condition $V()$ to all validators. Each validator verifies the validity of the message according to the customizable predicate $V()$. If $m$ passes the verification, the validator sends back to the sender a threshold-signed vote on $m$. The sender waits to collect a Byzantine quorum consisting of $2f+1$ votes, and then aggregates the signature shares into a single signature, referred to as a Quorum Certificate denoted $QC(m)$. Finally, the sender broadcasts the $QC(m)$ to all validators and they QC-deliver it.
-
For sender $s$ to QC-send($m, V$), send($m, V$) to all nodes.
-
Upon first message $(x, V)$ received by node $j$, if $V(x)$ send TE.Share-Sign($j, V, x$) to $s$.
-
Upon $2f+1$ valid TE shares $\sigma_i(x)$ received by sender $s$, set $QC(x) \gets$ TE.Sign($x, \sigma_1, …, \sigma_{2f+1}$) and send $QC(x)$ to all nodes.
- Upon a valid $QC(y)$ received by node $j$,
- in 1-phase protocol, QC-deliver($y$).
- in 2-phase protocol, set $lock \gets QC(y)$ and send TE.Share-Sign($j, QC(y)$) to $s$
- in 3-phase protocol, set $key \gets QC(y)$ and send TE.Share-Sign($j, QC(y)$) to $s$
-
Upon a valid $QC(QC(y))$ received by node $j$
- in 2-phase protocol, QC-deliver($y$)
- in 3-phase protocol, $lock \gets QC(y)$ and send TE.Share-Sign($j, QC(QC(y))$) to $s$
-
Upon a valid $QC(QC(QC(y)))$ received by node $j$
- in 3-phase protocol, QC-deliver($y$)
Algorithm 1. 1, 2, and 3 phases of Quorum Certified (QC) Broadcast.
2 QC-phases
Chaining 2 QC-phases, another round of validator voting is added. Each validator sends back to the sender a threshold-signed vote on $QC(m)$. Note that the validity predicate is not reinstanted in this case (except for standard format and signature verification, which is omitted), because the QC from the first phase guarantees it is valid.
The sender collects and aggregates the votes and broadcasts $QC(QC(m))$. A regime chaining 2 QC-phases is depicted in Figure 1 above (middle).
Importantly, the two phases are interpreted as lock and commit: We say that a validator commits $m$ if it QC-delivers $m$, and locks on $m$ if it votes on $QC(m)$. 2-phase provides the following lock-commit guarantee:
- Commit-Lock
-
if any validator commits $m$, then $2f+1$ validators are locked on $m$.
3 QC-phases
A 3-phase QC broadcast adds another identical phase and provides a stronger guarantee than lock-commit, referred to as key-lock-commit. We now say that a validator locks on $m$ if it votes on $QC(QC(m))$, and holds a key on $m$ if it votes on $QC(m)$. 3 QC-phases provide the following guarantees:
- Commit-Lock
-
if any validator commits $m$, then $2f+1$ validators are locked on $m$.
- Handover Responsiveness
-
if any validator is locked on $m$, then $2f+1$ validators hold a key on $m$.
3-phase QC is depicted in Figure 1 (bottom left) and a QC iconic representation (bottom right).
-
The literature also refers to CBC as secure broadcast. ↩



