From HotStuff to VABA
This post describes VABA by Abraham, Malkhi et al. [Abraham2019AsymptoticallyOV], the first tight upper bound for the Validated Byzantine Agreement problem in Asynchronous settings. The solution makes a direct use of HotStuff.
VABA borrows the template of Consensus solutions in the Partial Synchrony model. Specifically, it operates in a view-by-view manner, each view driven by a leader. If the leader is Honest, then the view is successful and the protocol terminates.
Using HotStuff as a building block, each view in VABA can be decomposed into two parts, as described in a previous post: first, leaders propose via VPCBC and second, a leader replacement is simplified and linearized using the Handover-Completion rule.
However, there is a twist. To prevent an asynchronous adversary from blocking every leader in its turn, Validators elect a leader at random via a distributed protocol to drive one view of HotStuff.
It might seem useless to elect a leader at random, because an Asynchronous adversary could delay messages from the designated leader during the iteration and cause it to fail. To thwart an Asynchronous adversary, VABA borrows a key idea from Katz and Koo in [@Katz2006OnEC]: Instead of a single view, it operates $n$ parallel-worlds of HotStuff, each with a different leader, and picks a “winning” one only after $2f+1$ of the worlds have already decided. This is where the linearity of HotStuff shines, the overall communication complexity is $O(n^2) = n \times O(n)$.
The Protocol
VABA operates in iterations, each consisting of three sub-procedures depicted below.
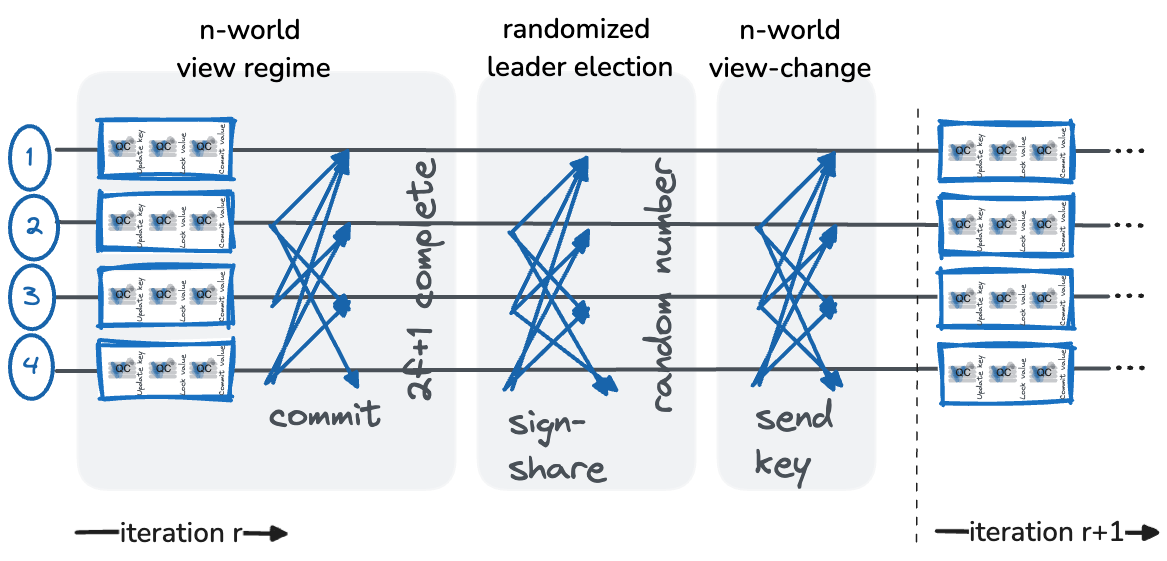
Sub-procedure 1: $n$-world HotStuff cores.
Validators operate $n$ instances of a single (non-pipelined) view of HotStuff in parallel, each instance with a different designated leader. Every Validator waits for $2f+1$ instances to terminate with a decision, which is guaranteed to eventually happen. Note, unlike the partial synchrony case, there are no view timers. Since each view sub-procedure of HotStuff has linear communication complexity, the overall communication complexity of operating $n$ parallel HotStuff views is $n \cdot O(n)$.
Sub-procedure 2: Randomized leader election.
Validators elect a winning instance (leader) in retrospect. Each participant $j$, after it completed $n-f$ instances, broadcasts a threshold-signature share $\sigma_j \leftarrow TE.ShareSign(j, iteration)$ to all other Validators. Each participant collects $n-f$ shares $\sigma_j$, combines them into a signature $\sigma \leftarrow TE.Combine(iteration, (\sigma_1, …, \sigma_{n-f}))$, and extracts a winning leader $\ell$ from the signature $\sigma$ via a deterministic function.
The communication complexity of this step is $O(n^2)$.
Importantly, all Validators complete this step with the same value, despite having completed potentially different subsets of $n-f$ instances in the first part. This is due to the properties of threshold encryption: the same value results by combining any subset of $n-f$ shares.
Sub-procedure 3: $n$-world HotStuff view-changes.
If a Validator decides in instance $\ell$, it broadcasts the decision to all other parties. Otherwise, it starts a new iteration $r+1$ in another $n$-world sub-procedure. Each one of the worlds operates a handover from the $\ell$ instance of iteration $r$ to a $j$ instance of iteration $r+1$.
The most important part to observe is that for any individual Validator, instance $\ell$ may not have terminated nor “expired”, since there are no view timers. Rather, receiving a result from the leader election stage signals that the Validator may stop activity in iteration $r$, akin to view expiration but without timers.
Once the winning instance $\ell$ has been received, the Validator stops participating in instance $\ell$ and proceeds with a view-change. It sends to the next iteration leaders in all worlds the highest QC the from instance $\ell$.
Since each view-change in HotStuff is linear, the communication complexity of $n$ parallel view-changes is $n \times O(n)$.
Analysis
It is fairly easy to see why this protocol has safety, because in the end, it operates view-by-view a HotStuff flow.1
Next, we concentrate on Liveness.
Liveness Requires Responsive Materialization of the Handover rule.
To see that VABA reaches a decision in expected contact time, consider two possibilities.
The first possibility is that the elected instance $\ell$ of the current iteration $r$ reaches a decision. We argue that this happens with constant probability: $f+1$ Honest parties must have each completed $n-f$ instances before the winning instance $\ell$ has been unveiled. Hence, picking one instance uniformly at random, one of the terminated instances with a commit decision is picked with probability at least $(f+1)\cdot(2f+1) / n \geq 2/9$.
The other possibility is that the winning instance $\ell$ does not reach a commit decision. In this case, all Validator will proceed with $n$ view-changes in parallel from iteration $r$ to $r+1$. Each one of the worlds in $r+1$ operates one instance of view change from the $\ell$’th instance of iteration $r$ to some instance of iteration $r+1$.
If there exists a Validator with a lock on the $\ell$’th instance, it is crucial that the leaders of the $r+1$ iteration will learn the lock. This is the Handover rule:
The Handover rule guarantees that when leaders start a new view, they learn the latest VPCBC lock which is held by any Honest Validator.
As explained in the Handover rule post, implementing this rule in Asynchronous settings with a 2-phase VPCBC regime requires quadratic communication. The importance of the 3-phase VPCBC regime is in providing a responsive implementation, that does not rely on bounded message transmission delays. This is the reason HotStuff, rather than HotStuff-2, is used in VABA: three-QC HotStuff guarantees that if a Validator holds a lock then $2f+1$ Validators have a QC on it. The next leader simply waits for highest QCs sent by $2f+1$ Validators.
-
Various details are omitted in the brief overview above; for more details, see the VABA whitepaper. ↩
